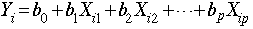
and provides tests of whether those coefficients are significantly different from zero.
The appropriate statistical procedure is multiple regression. More than one independent
variable is used to predict the dependent or outcome variable. Multiple regression estimates coefficients
for the interept and each predictor variable in the this equation:
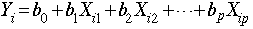
and provides tests of whether those coefficients are significantly different from zero.
We continue with the example of the candy bar data from the simple regression example. We want to know whether Total Fat, Carbohydrates, and Sugars (all measured in grams) predict Calories.
As a group, total fat, carbohydrates, and sugars (all measured in grams) significatly predict calories in candy bars (F(3, 71) = 1280, p < .0001), accounting for almost all of the variance (R^2 = 0.98). Holding constant or controlling for differences in the candy bars in terms of carbobhydrates and sugars, each additional gram of total fat predicts a significant increase in calories (t(71) = 55.6, p < .0001). Similarly, controling for total fat and sugars, each additional gram of carbohydrate predicts a significant increase of 4.3 calories (t(71) = 25, p < .0001). Finally and perhaps surprisingly, when controlling for total fat and carbohydrates, each additional gram of sugar predicts a significant decrease of about half a calories (t(71) = -2.5, p = .014). Because sugars are a type of carbohydrate, this suggests that non-sugar carbohydrates contribute more to calories than sugars themselves.
In this example, we assume that the candy dataset exists and has already been loaded as a table or data frame and attached, if necessary.
> candyMR <- lm(calories ~ totalFat + carbo + sugars)
> summary(candyMR)
Call:
lm(formula = calories ~ totalFat + carbo + sugars)
Residuals:
Min 1Q Median 3Q Max
-22.8271 -4.1305 0.3382 4.2962 19.6092
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.5695 4.4972 0.349 0.7281
totalFat 10.1216 0.1820 55.628 <2e-16 ***
carbo 4.3278 0.1734 24.954 <2e-16 ***
sugars -0.5290 0.2102 -2.516 0.0141 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 8.526 on 71 degrees of freedom
Multiple R-Squared: 0.9819, Adjusted R-squared: 0.9811
F-statistic: 1280 on 3 and 71 DF, p-value: < 2.2e-16
© 2002, Gary McClelland