The appropriate statistical test is a two-way between-subjects factorial analysis of variance (two-way ANOVA).
An experiment was performed to examine the effect of allowing students
to use calculators when solving SAT-type math questions. The experimenter
randomly assigned half of 18 particpants to use calculators and have to not
use calculators. Each group of 9 was further subdivided to work one of three
types of problems: Write--no choice answers are provided so the person must
write out a numerical answer with no hints; AorB--two mathematical statements (A and B)
are provided with choice options of 'A = B', 'A > B', 'A < B', 'can't be determined'; and Multiple
Choice--standard multiple-choice style questions. Each participant tries to answer 25 questions
of the type to be which they were randomly assigned. The following data result:
| Type | |||
| Calc | Write | AorB | MulCh |
| No | 11, 15, 13 | 16, 14, 15 | 18, 19, 17 |
| Yes | 10 14, 12 | 18, 19, 23 | 23, 19, 24 |
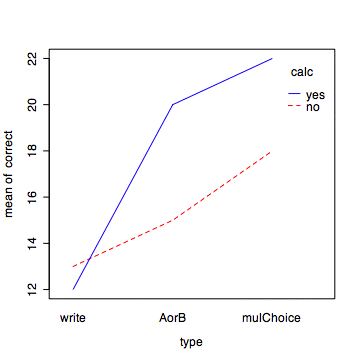
On average, across types of problems, the use of calculators improves performance on 25 math questions (M = 18 vs. M = 15.33, F(1,12) = 8.0, p = .015). Ignoring whether calculators were used or not, the three types of problems were not equally difficult (M = 12.5, M= 17.5, and M = 20, respectively for Write, AorB, and Multiple Choice problems, F(2,12) = 21.88, p < .0001). That is, problems for which choices were provided were easier than ones where the students wrote an answer with no hints. As can be seen in the interaction plot, the effet of calculators depended ( F(2,12) = 3.88, p = .0503) on the type of problem. For the Write problems there was essentially no difference in the number correct with and without the calculator (M=12 and M=13, respectively). However, for the problems with choices provided the benefit of calculators was sizeable--those using calculators answered an average of 4.5 more problems correct. Hence, calculators provide the most benefit when possible answers are available as choice options.
Either create a separate input file and read it in as a table or use the following commands for generating patterned data. The gl() function generates levels. The first number is the number of levels, the second number is how many consecutive levels should be generated before switching to the next level (or returning to the first level), and the last number is the total number of values to be generated. The commands below generate the table above by rows.
> calc <- gl(2,9,18, labels=c('no','yes'))
> calc
[1] no no no no no no no no no yes yes yes yes yes yes yes yes yes
Levels: no yes
> type <- gl(3,3,18, labels=c('write','AorB','mulChoice'))
> type
[1] write write write AorB AorB AorB mulChoice
[8] mulChoice mulChoice write write write AorB AorB
[15] AorB mulChoice mulChoice mulChoice
Levels: write AorB mulChoice
#now the depenent variable, by rows
> correct <- c(11,15,13,16,14,15,18,19,17,10,14,12,18,19,23,23,19,24)
#create a data.frame aggregating the the two level variables and the dependent variable
> calcData <- data.frame(calc, type, correct)
> calcData
calc type correct
1 no write 11
2 no write 15
3 no write 13
4 no AorB 16
5 no AorB 14
6 no AorB 15
7 no mulChoice 18
8 no mulChoice 19
9 no mulChoice 17
10 yes write 10
11 yes write 14
12 yes write 12
13 yes AorB 18
14 yes AorB 19
15 yes AorB 23
16 yes mulChoice 23
17 yes mulChoice 19
18 yes mulChoice 24
> #the notation calc*type is the same as calc + type + calc:type
> #or in other words, the two main effets and the interaction
> calc.aov <- aov(correct ~ calc*type)
> summary(calc.aov)
Df Sum Sq Mean Sq F value Pr(>F)
calc 1 32.0 32.0 8.000 0.01522 *
type 2 175.0 87.5 21.875 9.945e-05 ***
calc:type 2 31.0 15.5 3.875 0.05031 .
Residuals 12 48.0 4.0
---
Signif. codes: 0 Ô***Õ 0.001 Ô**Õ 0.01 Ô*Õ 0.05 Ô.Õ 0.1 Ô Õ 1
> # compute the means for each row
> tapply(correct, calc, mean)
no yes
15.33333 18.00000
> #now for each column
> tapply(correct, type, mean)
write AorB mulChoice
12.5 17.5 20.0
># finaly, compute the means for each cell
> tapply(correct, calc:type, mean)
no:write no:AorB no:mulChoice yes:write yes:AorB
13 15 18 12 20
yes:mulChoice
22
> interaction.plot(type, calc, correct, col=c('red','blue'))
In Excel, use Anova: Two-Factor With Replication in the Data Analysis Tools.
© 2007, Gary McClelland